Направления исследований
 |
| Зав. лаб. № 6 Алексей Гурьевич Кушнер |
Основное научное направление лаборатории – разработка методов исследования нелинейных систем с управлением, в частности, методов управления сингулярными режимами в распределённых системах. Такие системы описываются дифференциальными уравнениями в частных производных, как правило, нелинейными. Нелинейные системы с распределёнными параметрами встречаются во многих областях промышленности и науки: металлургии, реактивной технике, теплотехнике, медицине и др.
Основные методы исследования нелинейных систем, разрабатываемые в лаборатории, основаны на геометрической теории нелинейных дифференциальных уравнений, теории дифференциальных инвариантов, геометрии пространств джетов и теории особенностей.
 |
| Валентин Васильевич Лычагин (слева) и Иосиф Семёнович Красильщик |
Первые результаты в этих направлениях были получены в 1970-80-х годов в работах А.М. Виноградова, И.С. Красильщика и В.В. Лычагина. Их монография (Виноградов А.М., Красильщик И.С., Лычагин В.В. Введение в геометрию нелинейных дифференциальных уравнений. М.: Наука, 1986. 336 с.) по геометрии нелинейных дифференциальных уравнений явилась важной вехой развития этой области, определив направления последующих исследований.
Дальнейшее развитие методов геометрии дифференциальных уравнений отражено в монографиях А.Г. Кушнера, В.В. Лычагина, В.Н. Рубцова (Kushner A.G., Lychagin V.V., Rubtsov V.N. Contact geometry and nonlinear differential equations. Cambridge: Cambridge University Press, 2007. – 496 p.) и И.С. Красильщика, А.М. Вербоветского и Р. Витоло (Krasil'shchik J., Verbovetsky A., Vitolo R. The Symbolic Computation of Integrability Structures for Partial Differential Equations. Berlin, New York, London: Springer International Publishing, 2017. – 278 p.).
Основная идея геометрической теории дифференциальных уравнений состоит в их представлении как подмногообразий в пространстве струй (джетов) соответствующих порядков, а их решения – как специальных гиперповерхностей, лежащих в этих подмногообразиях. Это позволяет применить к исследованию уравнений в частных производных аппарат дифференциальной геометрии и гомологической алгебры, теории вариационных пуассоновых структур и дифференциальных накрытий.
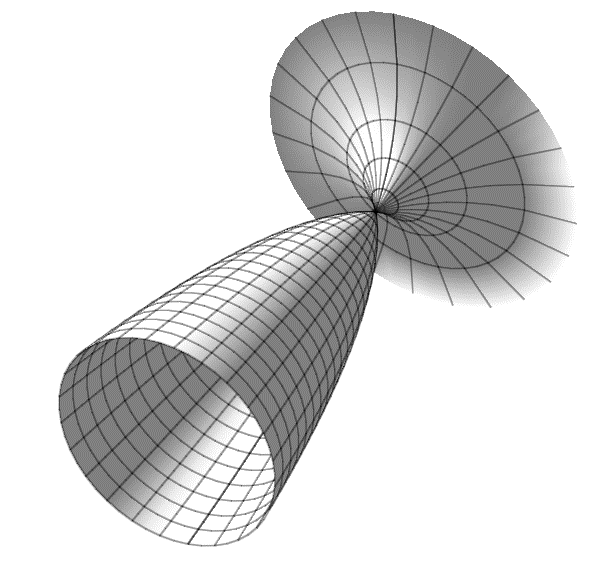 |
| Фокусировка звукового пучка |
Разработанные в лаборатории геометрические методы были применены к исследованию процессов течения газа и жидкости, распространению ударных волн в нелинейной акустике, задачам нелинейного теплообмена, к распространению волн в нелинейных средах и управлению этими процессами, а также к решению уравнений, возникающих в теории поля.
Перечислим основные результаты, полученные сотрудниками лаб. № 6 за последние несколько лет.
– Разработаны методы оптимального управления термодинамическими процессами, основанные на геометрическом представлении уравнений состояния среды лежандровым подмногообразием в соответствующем пространстве термодинамических переменных. Это позволило применить методы контактной геометрии.
– Проведена классификация возможных термодинамических состояний для трёхмерного уравнения Навье-Стокса, описывающее движение вязкой жидкости на многообразии, представляющем собой шаровой слой (модель атмосферы или океана), в зависимости от алгебры симметрий, допускаемых уравнениями состояния (Duyunova A., Lychagin V., Tychkov S. Differential invariants for spherical layer flows of viscid fluids // Journal of Geometry and Physics. 2018, Vol. 130. – pp. 288-292.
– Исследованы течения вязких жидкостей и газов с учётом фазовых переходов.
– Исследованы особенности многозначных решений задачи Коши для уравнений политропного течения сжимаемого газа.
– Разработан метод управления фокусировкой ограниченного акустического пучка в дисперсной среде.
– Для систем эволюционных дифференциальных уравнений в частных производных разработан метод построения конечномерных динамик, позволяющих находить асимптотически устойчивые режимы (А.В. Ахметзянов, А.Г. Кушнер, В.В. Лычагин. Аттракторы в моделях фильтрации // Доклады Академии наук. – 2017. – Т. 472, № 6. – С. 627–630.).
– Для систем с управляющими параметрами введены дифференциальные инварианты, названные инвариантами Петрова, и вычислены алгебры дифференциальных инвариантов для гамильтоновых систем с управляющими параметрами относительно преобразований обратной связи, что позволило провести их классификацию (А.Г. Кушнер, В.В. Лычагин. Инварианты Петрова гамильтоновых систем с управляющим параметром // Автоматика и телемеханика №3, 2013, 83–102.).
– Проведена классификация градиентных катастроф для решений системы двух нелинейных гиперболических дифференциальных уравнений первого порядка.
– Получена классификация гиперболических дифференциальных уравнений в частных производных с алгебраическими правыми частями относительно действия псевдогруппы точечных алгебраических преобразований.
– Доказана глобальная версия теоремы Ли–Трессе (B.S. Kruglikov, V.V. Lychagin. Global LieTresse theorem // Selecta Math. New Series, 22 (2016), No. 3, 1357–1411.). Эта теорема описывает структуру алгебры дифференциальных инвариантов продолженного в бесконечные джеты действия псевдогруппы Ли на расслоении. До этого теоремы типа Ли–Трессе существовали только в микролокальном виде или только для действия (конечномерных) групп Ли. Для доказательства этой теории были введены специальные типы алгебраических дифференциальных уравнений и алгебраических псевдогрупп Ли. Это специальные уравнения и псевдогруппы, которые задаются дифференциальными уравнениями, алгебраическими по производным, начиная с производных первого порядка. Стоит отметить, что уравнения и псевдогруппы Ли, встречающиеся на практике, относятся к уравнениям такого типа. В качестве первого, но далеко не тривиального результата, дано решение проблемы В.И. Арнольда о рациональности функции Пуанкаре в случае транзитивности действия на пространстве расслоения. Впоследствии теорема Ли–Трессе о дифференциальных инвариантах активно применялась для решения важных задач математической физики.
– Разработан оригинальный подход к задачам алгебраической теории инвариантов. Этот подход основан на использовании рациональных дифференциальных инвариантов вместо алгебраических и теореме Ли–Трессе, позволяющей эффективно находить дифференциальные инварианты. Вначале этот метод был применим к классической задаче об инвариантах бинарных форм, а затем и к произвольным k-формам. В дальнейшем, используя теорему Бореля–Вейля–Ботта, а также дифференциальные инварианты, была решена общая задача о разделении орбит действий полупростых алгебраических групп Ли в их неприводимых представлениях при помощи дифференциальных инвариантов (П.В. Бибиков, В.В. Лычагин. Классификация линейных действий алгебраических групп на пространствах однородных форм // Доклады Академии наук, 442:6 (2012), 732–735).
– Дифференциальные инварианты применены к проблеме распознавания образов. В частности, к проблеме распознавания отпечатков пальцев (V.V. Lychagin, N.G. Konovenko. Invariants of projective actions and their application to recognition of fingerprints // Analysis and Math. Physics. 6 (2016), No. 1, 95–107.).
– Построен и исследован аналог модели Бакли–Леверетта двухфазной фильтрации на гладких поверхностях и предложены методы решения задач оптимального управления для этой модели (Ахметзянов А.В., Кушнер А.Г., Лычагин В.В. Оптимальное управление разработкой нефтяных месторождений в модели Бакли–Леверетта // Автоматика и телемеханика. — 2018. — № 4. — С. 75–91.).
– На основе современных концепций нейрогеометрии построен универсальный эффективный алгоритм восстановления повреждённых изображений, включая сильно повреждённые (более 80 и даже 90 пикселов). Результат получен в сотрудничестве с французскими коллегами (U. Boscain, R. Chertovskih, J.-P. Gauthier, D. Prandi, A. Remizov. Highly corrupted image inpainting through hypoelliptic diffusion // Journal of Mathematical Imaging and Vision. 2018. Vol. 60, No. 8. pp. 1231-1245.).
История лаборатории
 |
| Основатель и первый зав. лаб. № 6 Георгий Михайлович Уланов |
Лаборатория была основана в 1961 г. и входила в состав отдела, возглавляемого академиком Б.Н. Петровым. На протяжении первых 26 лет лабораторией руководил д.т.н., проф. Георгий Михайлович Уланов. После его кончины заведующим лабораторией стал доктор технических наук В.П. Жуков. С 2010 г. лабораторией заведует д.ф.-м.н. Алексей Гурьевич Кушнер.
 |
| Виктор Павлович Жуков |
Первые годы работы лаборатории были посвящены исследованию проблем автоматического регулирования энергетических установок и маршевых ракетных двигателей, работающих с использованием ядерной энергии, а также автоматического регулирования систем жизнеобеспечения космонавтов в отсеках МКС и оптимального управления космическим кораблём с учётом неточностей реализации управления, повышения точности приземления космического аппарата, оптимального (по расходу топлива) управления системой ориентации космического аппарата. Эти работы проводились в соответствии с Постановлениями Правительства и по договорам с ведущими конструкторскими бюро. В частности, лаборатория участвовала в создании ряда эскизных проектов новых образцов отечественной техники и внесла значительный вклад в достижения отечественной космонавтики и оборонной техники.
Исторически одним из первых направлений фундаментальных исследований лаборатории в области теории управления явилась теория инвариантности, интенсивно разрабатывавшаяся в нашей стране в 50–60-е гг. прошлого века. Обобщением этой теории стала теория синтеза систем управления, обладающих заданными свойствами. Составной частью данной исследовательской работы был анализ идей Г.В. Щипанова по построению абсолютно инвариантных систем управления. Анализ показал принципиальную возможность создания инвариантных систем любой степени точности и указал условия достижения заданной точности.
В те же годы под руководством академика Б.Н. Петрова разрабатывались основы информационной теории управления, и в частности изучались вопросы пропускной способности информационно-измерительных систем и предельные возможности подобных систем.
В 70–90-х гг. ХХ века в лаборатории разрабатывались полевые методы исследования качественных свойств нелинейных динамических систем: асимптотической устойчивости, неустойчивости, существования инвариантных множеств, а также вопросы причинности, устойчивости и грубости систем управления распределёнными объектами.
Основным направлением научных исследований лаборатории с начала XXI века стала разработка методов исследования нелинейных систем, как с управляющими параметрами, так и без них. Это связано с приходом в лабораторию специалистов по геометрической теории дифференциальных уравнений В.В. Лычагина, И.С. Красильщика, А.Г. Кушнера, Д.В. Туницкого и их учеников.
 |
| Анатолий Григорьевич Бутковский |
В 2012 г. к лаб. № 6 была присоединена близкая по тематике лаб. № 63, которую основал и которой руководил более 30 лет д.т.н., проф. Анатолий Григорьевич Бутковский. В связи с этим лаб. № 6 вскоре было присвоено имя А.Г. Бутковского.
Лаборатория № 6 активно сотрудничает с лаб. № 19 Института в области оптимального управления процессом разработок месторождений углеводородов, с физическим факультетом МГУ им. М.В. Ломоносова, профессором которого является заведующий лабораторией А.Г. Кушнер, а также с математическими факультетами университетов Норвегии, Франции, Чехии, Польши, США, Колумбии и Италии.
В лаб. № 6 действует молодёжная научная школа под руководством Алексея Гурьевича Кушнера.
